Pairwiser runs a proprietary, state of the art algorithm for generating pairwise covering arrays. This post reports on the performance of this algorithm on a set of realistic and openly available test models.
Test Models
We collected a set of test models from studies of industrial software. Some of the models are of input parameters and some are of software product lines. All the models are large, industrial systems with a large amount of parameters, be it configuration parameters or input parameters with constraints between them.
In the study Variability Modeling in the Systems Software Domain, Thorsten Berger and colleagues made test models for eleven large, configurable, industrial systems. Among these are for example the Linux Kernel and firmware for consumer internet routers. These are some of the largest available models.
In the study Interaction Testing of Highly-Configurable Systems in the Presence of Constraints, Myra B. Cohen and colleagues provided test models for the input parameters of five software solutions including the GCC compiler collection and the SPIN simulator and verifier.
In the study Reverse engineering feature models, Steven She and colleagues made test models for three large, configurable, industrial systems: The Linux Kernel, eCos — a real-time operating system — and the FreeBSD kernel.
As can be clearly seen, these are large-scale industrial systems and are thus realistic case studies for the performance of an algorithm for generating pairwise covering arrays with respect to testing industrial systems.
The models are available for download here and here.
Test Machine
Pairwiser will run on a cloud service such as Amazon Web Services. Until this service has been set up, we benchmark on one of our development machines. It is a three year old high-end consumer desktop machine with the following specs:
- CPU: Intel Core i7-2600K @ 3,40GHz with Hyper Threading activated; it can run eight threads in parallel.
- Memory: 16 GB DDR3 @ 670 MHz
- Motherboard: ASUS P8P67 Deluxe
Test Results
The following results are from running the Pairwiser algorithm for generating pairwise covering arrays (Algorithm #237). All covering arrays were verified to have a coverage of 100% using the Pairwiser algorithm for coverage calculation (Algorithm #238, which performance will be the topic of a future blog post). If you would like to verify them yourself, the covering arrays are available for download here. We report the results are as follows.
- Parameters: Input or configuration parameters are originally modelled as having two or more options. Before running the algorithm, a test model is converted to conjunctive normal form (CNF). In the resulting formula, the parameters are modelled as binary parameters; their original nature is maintained using constraints. It is the number of binary parameters that is reported below (excluding the helper parameters introduced when converting to CNF).
- Cosntraints: Constrains are originally given as propositional formulas with basically and, or and not. Before running the algorithm, the constraints are converted to CNF. The number of clauses in the CNF formulas is reported below.
- Cases/Rows: A covering array consist of a number of rows; each row is a complete and valid assignment of the original test model. These assignments are such that every legal pair of combination of the test parameter values are in at least one row (i.e. pairwise). The number of rows in the covering arrays is reported below.
- Wall Clock Time: The wall clock time is the number of seconds taken to generate the covering array. The time is reported to give the number of seconds it actually took for the tester to get the result (i.e. as seen on the wall clock). The number of seconds allocated on the CPU for the algorithm by the OS was less in each case (see this table for all the details).
| Nr. | System | Parame-ters | Constraints | Cases (Rows) | Wall_Clock Time (s) |
|---|---|---|---|---|---|
| 1 | Linux Kernel (23 platforms) | 13 836 | 246 724 | 212 | 2 011,06 |
| 2 | Freetz | 6 848 | 101 877 | 82 | 211,15 |
| 3 | Linux Kernel (x86) | 5 701 | 187 193 | 616 | 315,65 |
| 4 | Buildroot | 3 672 | 45 575 | 117 | 58,29 |
| 5 | uClinux | 3 144 | 31 614 | 49 | 15,41 |
| 6 | EmbToolkit | 2 136 | 160 353 | 81 | 74,82 |
| 7 | BusyBox | 1 690 | 17 784 | 50 | 3,00 |
| 8 | FreeBSD kernel | 1 396 | 17 352 | 133 | 3,18 |
| 9 | coreboot | 1 386 | 47 090 | 40 | 2,60 |
| 10 | eCos | 1 244 | 2 768 | 113 | 2,24 |
| 11 | GCC | 220 | 41 | 30 | 0,07 |
| 12 | Apache | 210 | 8 | 43 | 0,10 |
| 13 | Spin Verifier | 93 | 50 | 54 | 0,03 |
| 14 | Bugzilla | 61 | 6 | 20 | 0,01 |
| 15 | Eclipse IDE | 48 | 615 | 35 | 0,02 |
This table holds a selection of the performance results. The measurements for more of the systems in the referenced studies are available in this table.
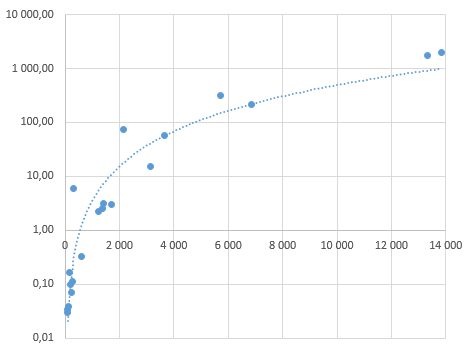
Plot
This plot shows test parameters vs. wall clock time (s).
Remarks
- The time taken to generate a pairwise covering array for Model 3 (Linux Kernel (x86)) is just 316 seconds (5.3 minutes). The previous documented record was published in An Algorithm for Generating t-wise Covering Arrays from Large Feature Models, where I and my colleagues generated a covering array in 33 702 seconds (562 minutes, or 9.4 hours) on a slightly different machine. Thus, the Pairwiser algorithm improves the performance of the best published algorithm by two orders of magnitude with respect to the Linux Kernel test model.
- There are algorithms, such as the one reported in An Improved Meta-Heuristic Search for Constrained Interaction Testing, that will generate a smaller covering array for, for example, Model 11 (GCC). However, the running time reported for that algorithm was 1902.0 seconds, which is significantly slower than Pairwiser’s.
- There are tools available online that generates covering arrays that are do not cover 100% of the pairwise interactions even though they claim to. Performance comparisons are only meaningful given that the generated models are verified to cover 100%. Even covering 98% might require significantly less resources. All results reported on here were verified to cover 100% of the pairwise combinations. If you would like to independently verify the covering arrays, they are available for download here.
References
- Thorsten Berger et al., Variability Modeling in the Systems Software Domain (2013)
- Martin F. Johansen et al., An Algorithm for Generating t-wise Covering Arrays from Large Feature Models (2012)
- Martin F. Johansen et al., Properties of Realistic Feature Models Make Combinatorial Testing of Product Lines Feasible (2011)
- Steven She et al., Reverse engineering feature models (2011)
- Brady J. Garvin et al., An Improved Meta-Heuristic Search for Constrained Interaction Testing (2009)
- Myra B. Cohen et al., Interaction Testing of Highly-Configurable Systems in the Presence of Constraints (2007)